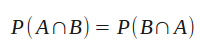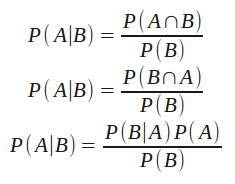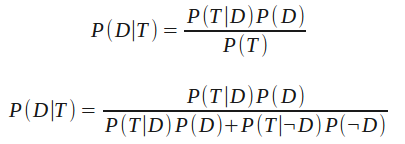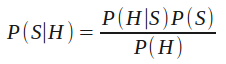By request, here’s my attempt to explain Bayes’ theorem (cribbing heavily from Wikipedia).
Deriving Bayes’ Theorem
We start with the standard definition of conditional probability (for events A and B):
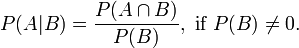
Which reads: The probability of event A given the known occurrence of event B is equal to the joint probability of events A and B (e.g., the probability of both events occurring) divided by the probability of event B (assuming the probability of B is not zero). I’m not going to show the derivation of conditional probability.
The summation axiom helps us understand the joint probability of A and B:
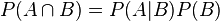
It tells us that the joint probability of A and B is equal to the probability of A given B multiplied by the probability of B. All we’re talking about is the likelihood of events A and B both occurring.
Keep the following equivalence in mind, we’ll need it in a minute. It simply says that the order of variables when writing the joint probability is irrelevant. It should be fairly straightforward that the likelihood of events A and B both occurring is the same as the likelihood of events B and A both occurring.
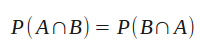
Filling back in our definition of conditional probability, we have (with the understanding that P(B) is not 0):
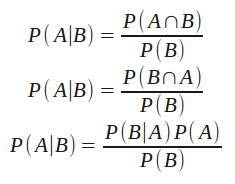
The third equation is the simplest form of Bayes’ theorem. It wasn’t very hard to get to and the math, relatively speaking, is quite simple (we’re not talking about deriving the Schrödinger equation or anything absurd). But its application, and understanding what it means, can be tricky.
P(A) is called the “prior,” representing our prior belief in the occurrence of event A.
P(A|B) is called the “posterior,” representing our belief in the occurrence of event A after (post) accounting for event B.
The remaining pieces, P(B|A) / P(B), are called the “support,” representing the support event B provides for the likelihood of event A occurring.
Applying Bayes’ Theorem
I’ll re-use the medical testing scenario from the previous post.
Substituting T to represent a positive test result and D to indicate the presence of the disease our equation becomes:
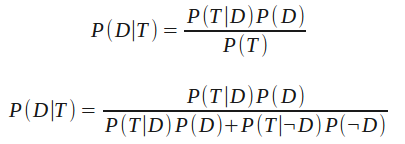
We expand P(T) into P(T|D)P(D) + P(T|¬D)P(¬D) which is to say: The probability of getting a positive test, P(T), is equal to [the probability of getting a positive test when the disease is present, P(T|D), multiplied by the probability that the disease is present, P(D)] plus [the probability of getting a positive test when the disease is not present, P(T|¬D), multiplied by the probability that the disease is not present, P(¬D)].
So now we just need to map the numbers we have about the disease and the test to the variables in our equation:
P(D), our prior, is 1 in 200 million–the disease occurrence rate in the general population.
P(T|D), the probability of getting a positive test when the disease is present, is derived from the false negative rate. When the disease is present, our test will only incorrectly say it is not 1 out of 200,000 times; so P(T|D) is 199,999 out of 200,000.
P(T|¬D), the probability of getting a positive test when the disease is not present is the false-positive rate: 1 in 100,000.
P(¬D), the probability of the disease not being present is simply the other 199,999,999 out of 200 million.
So let’s plug these numbers in step by step:
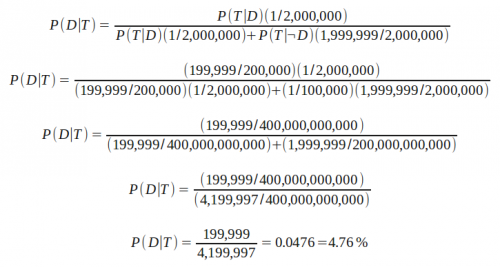
And we see that P(D|T), the probability that the disease is present given a positive test, is only 4.76%. (My previous post incorrectly reported this as 0.05%, I’ve corrected the error.)
The car example I presented didn’t use hard numbers, but I’ll frame the concept into Bayes’ Theorem. S will represent a car being stolen and H will represent a car being a Honda Civic:
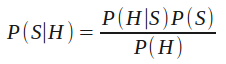
Which says, the probability that a car is stolen given that it’s a Honda Civic is equal to [the probability that a car is a Honda Civic given that it’s stolen] multiplied by [the probability of a car being stolen] divided by [the probability of a car being a Honda Civic].
The dealership was trying to push an insurance policy on me by only reporting P(H|S), but unless we account for the number of Honda Civics on the road in the first place, P(H), we aren’t getting the full story.
(Notice that we don’t have to actually care about P(S) if all we’re doing is comparing car make/models. P(S) doesn’t change for the different make/models so it doesn’t affect the relative rankings.)